BRAGG’S LAW

Diffraction of X-ray

The spreading of the ray from the corner or slit beyond the straight path is called diffraction. The diffraction of X–ray is discovered by Von-Lau in 1912 AD.

For the diffraction of X-ray, we need a slit or corner which has size in the order of the wavelength of X–ray. The wavelength of X–ray is in the order of 1Å. This size belongs to the size of the atom.

Thus, the diffraction of X – rays is possible only from crystals. The diffraction pattern of X- rays using Zinc Sulphide crystal is shown in the figure.

The X – rays produced from the Coolidge tube. These rays are passed from the slits to make the beam fine. The fine beam of X – rays is passed through the ZnS crystal. The X – rays are diffracted from the interatomic spacing and the diffraction pattern is observed in the photographic plate screen. The diffraction pattern helps to study the 3D distributions of atoms within the crystal.

Following are the conclusions of Von-Lau’s Experiment

(i) X-rays are electromagnetic waves.

(ii) The atoms in crystals are arranged in a regular three-dimensional pattern

Bragg’s Law:

Bragg’s law gives the mathematical description of diffraction of X–ray. Following are the assumptions for the diffraction of X–ray given by Bragg’s.

(i) When the beam of X-ray is passed through the crystal intense reflected X-ray is produced.

(ii)They interfere constructively when the path difference is equal to the integer multiple of the wavelength.

(iii)When constructive interference occurs, the diffracted beam of X – rays will leave the crystal at an angle

equal to that of the incident beam

Derivation of Bragg’s Formula

Consider three crystal planes of crystal XX’, YY’, and ZZ’ in which atoms are arranged in a regular pattern, as shown in the figure. Consider two X-rays AB and A’B’ incident on the plane of the crystal. A part of the X-ray is reflected and the remaining part is diffracted from the interatomic spacing. The diffracted ray is reflected from the lower plane and this process is similarly observed in the third plane. The reflected rays BC and B’C’ are shown in the figure.

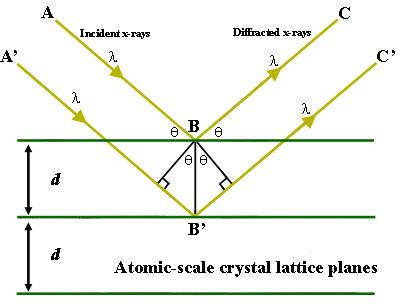
Let θ be the glancing angle of incidence and d be the distance between the crystal planes. Let us draw two perpendiculars from B on the ray A’B’ and B’C’ as shown in the figure. By geometry, ∡DBB’ and ∡EBB’ both are θ

. In the total course, the path difference between ABC and A’B’C’ is given by;

Path difference = DB’+ B’E

In △DBB’

sinθ = 𝐷𝐵’/𝐵𝐵’
= DB
= dsinθ

In △DBB’

sinθ = 𝐸𝐵’/𝐵𝐵’
=EB’
= dsinθ

Path difference = dsinθ+ dsinθ = 2dsinθ

According to Bragg, for the rays to interfere constructively, to give a diffraction pattern, the path difference between them is an integer multiple of the wavelength.

i.e., 2dsinθ = nλ

where, n = 0,1, 2, 3, 4, 5, ……. and λ be the wavelength of X–ray.

In general,

2dsinθn = nλ …….(i)

Equation (i) is the Bragg’s equation for diffraction of X–ray through the crystal.