WAVE MOTION

Periodic motion: The motion which repeats in an equal interval of time is called periodic motion. For e.g. Rotation and revolution of the earth, hands of the clock, heartbeat, simple and compound pendulum.. etc
Simple harmonic motion: The motion of two attributes i.e. periodic and oscillatory motion is the simple harmonic motion. For e.g. simple pendulum, mass-spring system, the motion of particles during the propagation of sound, etc.
                  DEFINITIONS RELATED TO WAVE MOTION
                                              y = a sin (wt–kx)
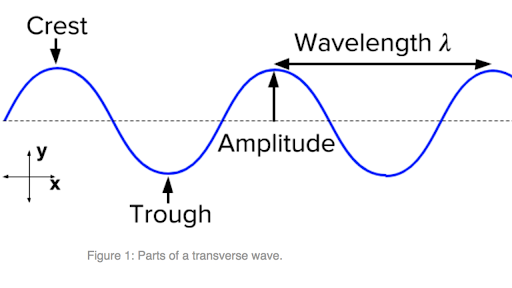
•Displacement (y): Distance of vibrating particle from its mean position.
•Amplitude (a): Maximum displacement of a particle from its mean position.
•Wavelength (λ): the distance between two nearest particles vibrating in the same phase. [distance between two consecutive crests or troughs, OR, two consecutive compressions or rarefactions]
•Time period (T): Time in which a particle completes one vibration about its mean position.
•Frequency (f  or n): The number of waves produced per unit time (f = 1/T).
•Angular frequency (w): The rate of change of phase of a particle with time (w =2π/T = 2πf).
•Propagation constant or angular wavenumber (k) = 2π/λ.
•Phase velocity(wave ): Distance covered by a wave per unit time in its direction of propagation. A wave completes one oscillation in time T and travels a distance λ (v = λ/T = f λ).                                                                      •Particle velocity: Vp = ω√(a^2-b^2), it is variable and depends on displacement.
•Phase: The angular displacement that describes the state of motion of the particle is called its phase. Generally, it is expressed in terms of an angle so it is also called the phase angle. (ø = ωt ± kx).
Types of oscillations
(i) Free oscillations free vibration, the amplitude is constant with time.                                                                                    (ii) Damped oscillations Amplitude of oscillation decreases with time and finally becomes zero.                                iii) Forced oscillations Vibrating body is maintained in the state of vibration by a periodic force of frequency (n) other than its natural frequency of the body.
*Resonance is a phenomenon in which the frequency of the external periodic force is equal to the natural frequency of oscillation of the system, then the amplitude of oscillation will be large.
                                                        Wave Motion                                                                                                                                               Wave:                                                                                                                                                                                                                       Wave is a disturbance that travels from one region of a medium to another. In wave motion, there is the transfer of energy without transport of matter.                                                                                                                                                                                                            Types of wave:
1)On the basis of medium required for propagation):                                                                                                                a)Mechanical wave / Elastic waves: That require material medium for their propagation are called Mechanical waves. They cannot transmit in vacuum.E.g. Sound waves, Vibration in a stretched string, ripples on a pond, etc.
b) Electromagnetic Wave / Non-mechanical wave: The waves which do not require material medium for their propagation are called Electromagnetic wave. They can transmit in a vacuum. E.g.. Lightwave, X-rays, Gamma rays, etc.
  2) On the basis of the vibration of particles
  a) Transverse wave:
The wave in which the particles of the medium vibrate about their mean position perpendicularly to the direction of propagation of the wave is called a Transverse wave. Such wave propagates in the form of crest and trough. These waves can propagate on only those mediums which can sustain shearing stress. E.g.. Waves produced on plugging a stretched string, rod, electromagnetic waves, waves on the surface of the water, waves in-stadium, etc.                                                                                                                                                                                  b)Longitudinal waves;                                                                                                                                                                                                                                        The wave in which the particles of the medium vibrate along the direction of propagation of the wave is called a Longitudinal wave. Such wave propagates in the form of compression and rarefaction. These waves can propagate on that medium which can sustain compressive stress. For eg. Sound waves, Seismic P-waves, Waves in spring, etc.
PROPERTIES OF MEDIUM FOR PROPAGATION OF WAVE
1)Elasticity(for the particles to return to their mean positions after being disturbed)
2)Inertia or mass (so that particles can store kinetic energy)
3)Minimum frictional resistance (otherwise the vibrational motion of the particle may be damped).
CHARACTERISTICS OF WAVE MOTION
•It is the disturbance caused in a medium by the repeated motion of particles of the medium.
•When a wave travels forward, the particles of the medium vibrate about their mean position.
•A particle receives energy from the previous particle and hands over some energy to the next particle.
•Each particle in the medium starts vibrating a little later than the preceding one.
•The wave travels with the same velocity but the velocity of the particle varies with its position.
          RELATION BETWEEN PHASE DIFFERENCE AND PATH DIFFERENCE
The difference in angular displacement between two points(waves) is called phase difference and the linear distance between them(points/waves) is called path difference.
The phase difference between points O(origin ) and A is 2π and the path difference between them is λ. Comparing any point P with other point O from the figure,
For path difference, a λ phase difference is = 2π
For path difference unity phase difference =2π/λ
For path difference, x phase difference is =2π*(x)/λ
Phase difference( Φ) =2π*(x)/λ
Very Important  Question(VIQ). Define progressive waves. Derive progressive wave equation in a medium.
Progressive wave:
The wave that travels from one region to another region of a medium is called a Progressive wave. Progressive waves may be transverse or longitudinal.
Equation of Progressive wave:
Consider a wave is traveling from left to right along the x-axis as shown in figure aside. Let a particle at origin ‘O’ is vibrating simply harmonically and its displacement at any instant of time ‘t’ is given by
y = a sin ωt——-(1)
where a is the amplitude of the particle and ωis its angular velocity. Now, let us consider another particle ‘P’ at a distance ‘x’ from O. Since the particle P receives the disturbance later than the particle at ‘O’, the phase of the motion of particle P lags to that of ‘O’.
If ϕbe the phase difference of the particle P, then its displacement at the given instant of time ‘t’ is given by
y = a sin (ωt –ϕ) —–(2)
For a path difference of ‘X’, the phase difference is= 2π                                                                                                                 For a path difference of 1, the phase difference is= 2π/λ                                                                                                             For a path difference of ‘x’, the phase difference is    =2π*(x)/λ
ø=2π*(x)/λ                      ——– (3)
substituting eq. (3) in eq.(2)
y = a sin(ωt –2πx/λ  )           —-(4)
or,y = a sin (ωt –kx)          ——- (5)
where k =  2πx/λ  is called number or propagation constant
Since, ω =  2π/T, eq (4) can be expressed as
y = a sin(2πt/T –2πx/λ  )
y = a sin2π(t/T –x/λ  ) ———-(6)
we know, ω =2πf=2πv/λ. Now, eqn (4) becomes
y = a sin(2πvt/λ   -2πx/λ  )
∴  y = a sin2π/λ(vt  – x)      ———–(7)                                                                                                                                                    Eq. (6) and (7) are the equations of a plane progressive wave.                                                                                                        If the wave travels from right to left then vibration at ‘P’ leads that to that at O. Hence, in this case, the equation of progressive wave becomes.
∴  y = a sin2π/λ(vt  + x)
IN GENERAL y = a sin (ωt  ±kx)
Short questions:
  1)Frequency is the most fundamental property of a wave. Why?
Ans: Frequency is the most fundamental property of a wave because when a wave passes from one medium to another, its velocity and wavelength changes but the frequency remains the same.
2) Longitudinal waves are also called pressure waves, why?
Ans: Longitudinal wave propagates through the medium in the form of compression and rarefaction. Propagation of longitudinal waves involves the change in pressure and volume. So, longitudinal waves are also called Pressure waves.
3) If you are walking on the moon surface, can you hear the cracking sound behind you? Explain.
Ans: For the propagation of the sound waves, the material medium is necessary. On the surface of the moon, there is no atmosphere so it not possible to hear a cracking sound behind you while walking on the moon surface.
4) Which type of wave propagates in liquid? Explain.
Ans: For the propagation of the transverse wave, the medium should possess a modulus of rigidity whereas, for the propagation of the longitudinal wave, the bulk modulus of the medium is responsible. Liquids have only bulk modulus so longitudinal waves can propagate through a liquid. However, Transverse waves can propagate on the surface of a liquid as the liquid surfaces possess surface tension.
Principle of Superposition Of waves:
The principle of Superposition states that” When two or more waves are passing through a medium at the same time, the resultant displacement at any point is equal to the vector sum of their individual displacements at that point.”
If y1, y2, y3, . . . ., yn be the displacements at a point due to individual waves, then the resultant displacement ‘y’ at the same time when the waves superpose to each other is given by
y = y1 + y2 + y3+ . . . . . + yn
Note: The principle of superposition can be used to explain many wave phenomena which are:                                  a) When two waves of the same frequency moving in the same direction superpose, interference of waves is obtained.
b) When two waves of the same frequency moving in opposite direction superpose, stationary waves are produced.
c) When two waves of slightly different frequencies are traveling in the same direction superpose, beats are produced.
Stationary wave / Standing wave:(very very important)
When two progressive waves of the same amplitude and frequency travel through a medium with the same speed but in opposite direction are superposed, the resultant wave is called a Stationary wave.
Stationary wave ( Standing waves) is called so because the waveform does not travel along in either direction.
REFLECTION, REFRACTION, INTERFERENCE, DIFFRACTION, AND POLARIZATION OF SOUND
Like light sound, wave exhibits phenomena like reflection, refraction, interference, and diffraction. These properties are common to both sound and light but polarization is the phenomenon shown by transverse waves but not by longitudinal waves. The sound being a longitudinal wave does not diffract because the vibration of particles is along the direction of propagation of waves which cannot be restricted in a particular plane.
1) How are stationary waves formed?
Ans: When two progressive waves of the same amplitude and frequency travel through a medium with the same speed but in opposite direction are superposed, the resultant wave is called a Stationary wave.